Teorie

Algebra problémů

Během procesu myšleni rozkládáme složitou objektivní realitu - okolní svět - na jednotlivé objekty. Objekt je definovaná část objektivní reality a bude nadále označován velkými písmeny X, Y, Z. Objekty mohou být velmi malé jako např. elementární částice, kvanta světla, atomy, molekuly, buňky nebo značně velké jako člověk, dům, město, stát, planeta, atd. Místo o objektu Z můžeme uvažovat o dvou objektech X a Y přičemž v obou případech jde o stejnou část objektivní reality, nebo naopak místo o objektech X a Y můžeme uvažovat o objektu Z - tyto operace se nazývají skládání a rozkládání objektů. Můžeme si představit celý vesmír X₀ rozložený do objektů X₁,X₂,X₃...X_N tak, že složení těchto objektů je celý vesmír (X₁ X₂ X₃... X_N=X₀). Takovou množinu O = {X₁,X₂,X₃...X_N}můžeme nazývat množinou všech objektů.

Stav objektu je uspořádání vnitřních částí objektu a jeho poloha, rychlost a další parametry v jednom okamžiku. Pokud je možné popsat stav objektu X veličinami (fyzikálními, chemickými nebo jinými)  Q₁,Q₂,Q₃...Q_n hodnoty x₁, x₂, ... x_n těchto veličin lze považovat za souřadnice v n-rozměrném prostoru nazývaném fázový prostor. Každý bod fázového prostoru reprezentuje jeden stav objektu X. Hodnoty x₁, x₂, ... x_n jsou složky stavového vektoru . Objekt X ve stavu je označován X(). S přesností definovanou veličinami Q₁,Q₂,Q₃...Q_n fázový prostor reprezentuje všechny možné stavy objektu X.

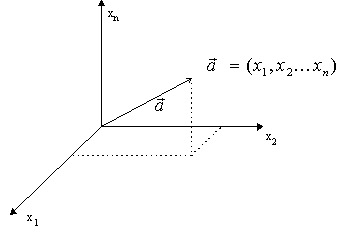
Kdykoli děláme nějakou práci, něco nám vadí nebo bychom rádi dosáhli nějakého cíle, podstata tohoto může být přesně popsána definováním části objektivní reality (takzvaného problémového objektu) a definováním dvou stavů (výchozího -nepříznivého a konečného - žádoucího) této části objektivní reality. Proto je problém obecně definován jako uspořádaná dvojice stavů nějakého objektu symbolicky X[,] [X(), X()]. 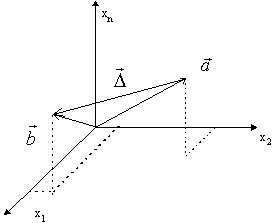Vektor se nazývá výchozí stavový vektor, konečný stavový vektor, -(delta) vektor změny stavu. Ve fázovém prostoru objektu X je problém reprezentován dvojicí bodů s definovaným pořadím.

Problémy můžeme skládat nebo rozkládat sériově ( X[,] + X[,] = X[,] ) nebo paralelně ( X[,] + Y[,] = Z[,] ; XY=Z ). Inverzním problémem k problému X[,] je nazýván problém X[,]. Nulový problém je takový problém X[,] pro nějž = . Složením problému a problému inverzního vzniká nulový problém (X[,] + X[,] = X[,]). Pokud výchozí stavový vektor odpovídá současnému (přítomnému) stavu objektu X, problém X[,] se nazývá aktuální, v opačném případě se nazývá virtuální. Řešení problému X[,] je obecně vnější silové působení, které způsobí, že objekt X změní svůj stav z  do . Složení řešení jednotlivých podproblémů je jedním z možných řešení složeného problému.

Biologie problémů

Abstraktní problémy se mohou zrcadlit (ztělesňovat) v neuronové síti lidského mozku: představa objektu X ve stavu který chceme změnit nebo ve stavu který bychom rádi dosáhli, nebo oboje, jsou realizovány nervovým impulsem v našem centrálním nervovém systému. Přesněji za "ztělesnění" problému X[,] můžeme považovat dvě neuronové smyčky, kterými periodicky prochází nervový impuls.

Protože pokus vyřešit dobře definovaný problém X[,] za daný časový interval T má jednoznačný výsledek (ano/ne) je řešitelnost problému měřitelná, časově a na člověku závislá veličina. Symboly S(t) a N(t) označují množinu všech řešitelných resp. neřešitelných problémů.

Problémy ovlivňují nespokojenost nebo spokojenost lidí. Nespokojenost může být popisována biochemickou veličinou GS (globální stav) definovatelnou na základě množství chemických, elektrických a dalších veličin měřitelných v našem centrálním nervovém systému. GS může nabývat hodnot 0 (spokojenost) až GS_max (extrémní nespokojenost), a může být sledována jako funkce času GS = GS(t). V příkladu na obrázku se v čase  t_A a t_B objevily nějaké problémy a způsobily nárůst nespokojenosti:

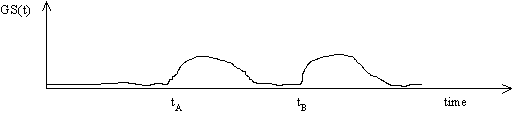
Místo jako časově závislá, veličina GS (popisující nespokojenost) může být sledována jako funkce stavu objektu GS = GS(X()) definovaná pro všechny stavy všech objektů, protože různé stavy různých objektů nám přinášejí různou nespokojenost. V lidském mozku je propojení X() <=> nespokojenost GS(X()) realizováno neuronovými spoji mezi oblastí realizující představu objektu X ve stavu  a oblastí generující emoce (emotion related structure).

Význam GS problému X[,] je definován jako  GS(X[,]) = GS(X()) - GS(X()) a je na člověku závislou a měřitelnou veličinou. Říká něco ve smyslu, jak moc se zlepší naše spokojenost, když vyřešíme problém X[,].

Neuronová spojení realizující význam problémů jsme buď zdědili nebo byla vytvořena v průběhu našeho života naším vlastním subjektivním myšlením. V každém případě minimální možný význam je nula, protože libovolný z těchto neuronových synaptických spojů má biologickou schopnost rozpojení (relaxace). Proto přesně platí takzvaný obecný princip subjektivity problémů:

GS_min(X[,],t) = 0; X[,], t

"Význam libovolného problému je pouze subjektivní" - jinými slovy objektivní význam (definovaný jako minimální subjektivní význam) libovolného problému v libovolném okamžiku je nula. To znamená , že můžeme v okamžiku t zůstat zcela spokojeni i když problém X[,] nebudeme řešit.

Obecný princip subjektivity problémů nepřináší žádný praktický užitek, protože považování všech problémů za objektivně bezvýznamné by zvýšilo naši nespokojenost (většinou je výhodnější problém místo toho prostě vyřešit). Minimalizací příspěvku náhodného problému k nespokojenosti nalezneme takzvaný zúžený princip subjektivity problémů (nazývaný zkráceně "princip subjektivity problémů"):

X[,] N(t) GS_min(X[,],t) = 0; t

t.j. problém, který není řešitelný v okamžiku t, je v tom okamžiku významný pouze subjektivně (zdánlivě) (nebo jinak každý problém je v okamžiku t buď řešitelný nebo je v ten moment objektivně bezvýznamný). Důvodem exaktní platnosti tohoto tvrzení je objektivně existující (biologická) možnost úplného rozpojení neuronových vláken implementujících "důležitost problému". Tento princip je nazýván "zúžený" protože zužujeme (redukujeme) tvrzení obecného principu subjektivity pouze na množinu všech neřešitelných problémů. V tvrzení principu subjektivity problémů nejsou žádné rozpory, a to ani v blízkosti naší smrti, protože tato zákonitost má diferenciální charakter v čase (je vztažena k jednomu okamžiku) a spokojenost (tedy určitý globální stav našeho mozku) v přítomném okamžiku je považován za základní hodnotu, k níž je vše ostatní připojeno pomocí neuronových spojů.

Princip subjektivity problémů si můžeme zapamatovat např. takto:

nebo takto:

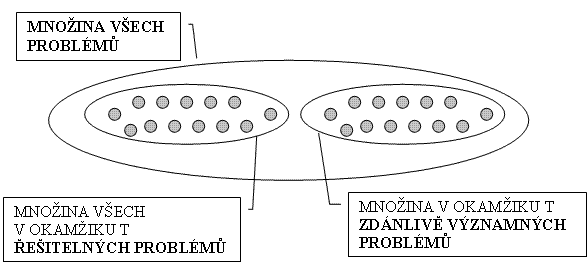
A na závěr logická konstrukce množiny všech problémů: